Standing Waves Part II
Problem 1
An ideal taut string of length \( l \) and mass \( m \) is attached to a fixed point at one end and to a massive ring of mass \( M_R \) at the other end as shown below. The ring is free to move on a horizontal frictionless rod which is perpendicular to the string in its equiibrium position. The tension in the string, \( T \), can be considered constant at all times and gravity can be ignored.
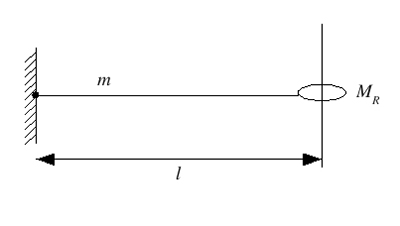
- Starting with the general form of the normal mode solutions of the classical wave equation for a taut string, derive an equation which, when solved, gives the angular frequency \( \omega \) of the lowest mode of the system. YOU ARE NOT ASKED TO SOLVE THIS EQUATION.
- Determine the angular frequency of the lowest normal mode for
- \( M_R = 0 \)
- \( M_R = \infty \).
› View/Hide Answers
Problem 2
A system consists of two materials glued together at \(x = L\) and subject to longitudinal (sound) wave propagation. The end at \(x = 0\) is fixed and the end at \(x = 4L\) is free. A tungsten-lead alloy is used for the segment \(0 \leq x \leq L\), with a Young's modulus of \(Y = 7 \times 10^{10}\) N/m\(^2\) and density \(\rho = 14.4 \times 10^{3}\) kg/m\(^3\), while the segment \(L \leq x \leq 4L\) is comprised of a carbon fiber alloy that is as strong as the tungsten-lead alloy with \(Y = 7 \times 10^{10}\) N/m\(^2\) but nine times less dense, with \(\rho = 1.6 \times 10^{3}\) kg/m\(^3\).
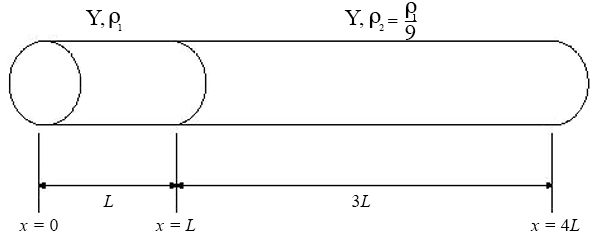
- Derive a condition for the normal mode frequency of longitudinal oscillation, \(\omega_n\), of the two-metal system.
- Evaluate the frequencies for the first four modes, in terms of the length \(L\).
› View/Hide Hint
› View/Hide Answers
