Problems

Standing Waves Part I

Problem 1

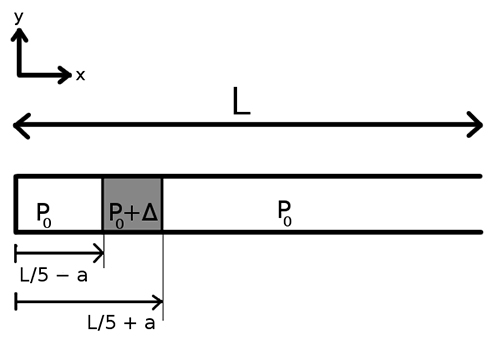
The figure above shows a long tube filled with air. The end located at \(x=0\) is closed with a cap, while the opposite end, located at \(x=L\) is open to the atmosphere. There are two thin membranes, one located at \(L/5 - a\), while the other is located at \(x= L/5 + a\), with \(a \ll L\). In between the membranes (in the shaded region) the air pressure is a constant \(P_0 + \Delta\). At time \(t=0\) the membranes are broken.

1. What is the amplitude of the \(n\)-th normal pressure mode of this tube (without the membranes), regardless of whether or not it is excited?
   

   › View/Hide Hint

   The boundary conditions are \( \dfrac{dP}{dx} = 0\) at \(x = 0\) and \(P = 0\) at \(x = L.\)

    

2. After the membranes are broken what is the lowest normal mode that is not excited?
3. Now suppose the end of the tube at \(x=0\) has the cap removed. How would your answer for part (2) change?
   

   › View/Hide Hint

   This part of the problem can be done without lengthy calculations.

Problem 2

An ideal taut string of length \( 2L \) is fixed at both ends. At time \( t = 0 \) it is stationary and distorted as shown below and is then released. The distortion can be decomposed into its Fourier components.

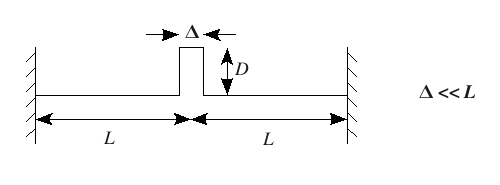
1. Derive an expression for the amplitude of the lowest frequency component. Your answer must not contain unevaluated integrals.
2. Prove that the components with the largest amplitude satisfy \( \lambda \gg \Delta \) where \( \lambda \) is the wavelength of the component, and that the amplitude of these components is approximately independent of \( \lambda \).

« Previous | Next »