Problems | Harmonic Oscillators with Damping | Problem Solving Videos | Vibrations and Waves Problem Solving

Harmonic Oscillators with Damping

Problem 1

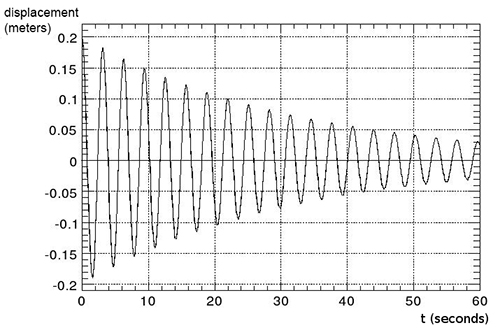
Using a force of 4 newtons, a damped harmonic oscillator is displaced from equilibrium by 0.2 meters. At t = 0 it is released from rest. The resultant displacement of the oscillator, from the equilibrium position, as a function of time, is shown in the figure below. Estimate, as well as you can using the given information:

The mass of the oscillator.
The quality factor of the oscillator.

Graph showing results of displacement on the y axis and time on the x axis. The oscillations gradually move from large displacement to small displacement in sixty seconds.

› View/Hide Answer

Problem 2

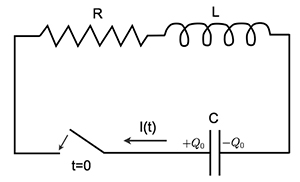
An RLC circuit with switch open at time zero.

The circuit shown above consists of a capacitor ( $C$ ), an inductor ( $L$ ) and a resistor ( $R$ ). Initially the switch is open and the charge ( $Q$ ) on the capacitor is $Q(t \leq 0) =Q_0$ . At $t = 0$ , the switch is closed.

For what values of $R$ , the initial sign of $Q(t)$ will be reversed at some later times?
Assuming that the value of $R$ satisfies the condition in (1), find $Q(t)$ and the current $I(t)$ in terms of $Q_0$ , $R$ , $L$ and $C$ . Draw qualitative sketches of both $Q(t)$ and $I(t)$ . (Make sure to indicate the behaviour around $t=0$ ).
If it takes 10 cycles for the energy in the circuit to decrease to $1/e$ times its initial value, find the value of the resistance $R$ in terms of $L$ and $C$ .

› View/Hide Answers

1. Initial sign will be reversed only if the circuit is underdamped:

i.e., $R < 2 \sqrt{\frac{L}{C}}$

$Q(t) = Q_{0} e^{-\frac{\gamma t}{2}} \left(\cos(\omega't) + \frac{\gamma}{2 \omega'} \sin(\omega't)\right)$ and

$\begin{align*} I(t) &= \omega' Q_{0} e^{-\frac{\gamma t}{2}} \sin(\omega't) + \frac{\gamma}{2} \frac{Q_{0}\gamma}{2 \omega'} e^{-\frac{\gamma t}{2}} \sin(\omega't)\\ &= Q_{0}\frac{\omega_{0}^{2}}{\omega'}e^{-\frac{\gamma t}{2}} \sin(\omega't). \end{align*}$

$\begin{equation} \nonumber{\text{where} \hspace{4mm} \gamma = {\frac{R}{L}} \hspace{1mm} \text{,} \hspace{4mm} \omega_{0}^{2} = {\frac{1}{LC}} \hspace{4mm} \text{and} \hspace{4mm} \omega'=\sqrt{\omega_{0}^{2}-\frac{\gamma^2}{4}}} \end{equation}$

Below are the sketches of

$Q(t)$ and

$I(t)$ . Note that

$I(0)=0$ and both

$Q(t)$ and

$I(t)$ oscillate at the same frequency.

Two graphs showing results of displacement on the y axis and time on the x axis. The first graph shows the current and the second shows the charge.