Driven Harmonic Oscillators
Problem 1
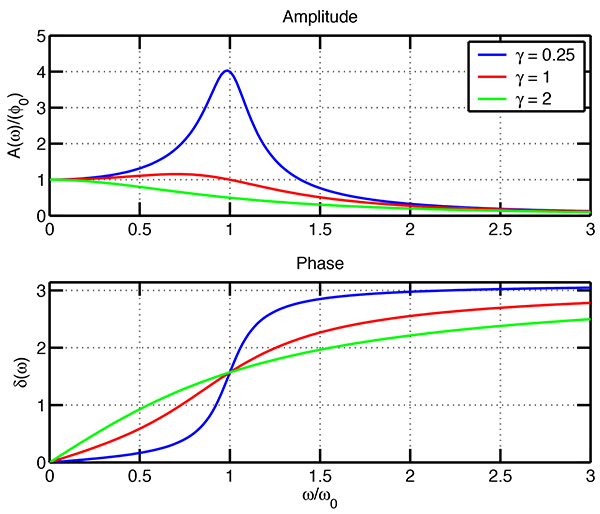
A torsional oscillator comprises a cylinder with moment of inertia, \(I\), hanging from a light rod with torsional spring constant, \(\kappa\). The cylinder also experiences a drag torque equal to \(-\mu \dot \theta\), when moving with angular velocity \(\dot \theta\). The top of the rod is driven with angular displacement \(\phi(t) = \phi_0 \cos{\omega t}\).
- Find the steady-state solution for \(\theta(t)\).
- Plot the amplitude \(A(\omega) \) and phase \(\delta(\omega)\) of your solution for \(\theta(t)\) in (1) as a function of \(\omega\). For your plot, assume that the natural frequency of oscillation of the system \(\omega_0 = 1\), and plot three curves on the same plot with \(\frac{\mu}{I} = 0.25\), 1 and 2. Label your curves to distinguish the three cases.
› View/Hide Answers
Problem 2
A capacitor (of capacitance C), a resistor (of resistance R) and an inductor (of inductance L) are connected to an AC voltage source \(V = V_0 \sin(\omega t)\) starting at \(t=0\) as shown in the diagram below.
Assuming that both the current and the charge of the capacitor are initially zero, determine the expression for \(V_C(t\ge0)\) with \(\omega=\omega_0=\dfrac{1}{\sqrt{LC}}\) and \(L < 4R^2C\).
› View/Hide Answer