Accelerated Charges Radiating Electromagnetic Waves
Problem 1
Electrons with charge \(e\) are accelerated from a negative plane electrode toward one parallel to it, at a potential \(V_0\). The mass of the electron is \(m\) and the plates are separated by a distance \(d\). Assume that the energy loss due to radiation is much smaller than \(eV_0\) and the velocity of the electron at all times is small compared to the speed of light \(c\). Calculate the energy radiated during the acceleration as a fraction of the energy with which it would strike the positive electrode in the absence of radiation.
› View/Hide Answer
Problem 2
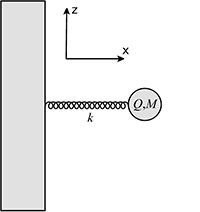
A charged particle of mass \(M\) and charge \(+Q\) is attached to the end of an ideal spring of spring constant \(k\). The spring is constrained to lie along the \(x\)-axis and at equilibrium the particle is at the origin. The particle is displaced from equilibrium by a distance \(A\) in the \(x\) direction, and released at \(t=0\). Assume that the size of the particle is much smaller than \(A\), so it can be treated as a point charge and that the damping rate is very small. Assume also that the structure and spring have no electromagnetic interactions with the charge Q or radiated field.
- Calculate the electric field radiated by the particle along an arbitrary well defined direction in the \(x-z\) plane, at a distance R, where \(R \gg A\).
- Calculate the total time averaged power radiated by the particle.
- Assuming that the power radiated does not change appreciably as a function of time, give a simple rough estimate of the time it will take for the particle to decrease its amplitude of oscillation to \(1/e\) of its initial value. Is this assumption realistic?
› View/Hide Answers
