Most of the problems are assigned from the required textbook 
Bona, Miklos. A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory. World Scientific Publishing Company, 2011. ISBN: 9789814335232. [Preview with Google Books]
A problem marked by * is difficult; it is not necessary to solve such a problem to do well in the course.
Problem Set 11
- Due in Session 33
- Practice Problems
- Session 30:
- Let G be a bipartite graph with bipartition (X,Y). Show that the following three conditions are equivalent.
- G is connected, and each edge of G is contained in a perfect matching.
- For any x in X and y in Y, G-x-y has a perfect matching.
- X = Y, and for every nonempty subset T of X except X, we have N(T) > T.
- Let M be an m×n matrix of 0's and 1's. Let a(M) be the maximum number of 1's of M such that no two are in the same row or column. Let b(M) be the minimum number of rows and columns of M such that cover every 1 (i.e., every one is in at least one of the rows or columns). Show that a(M) = b(M). (Hint. Use the Konig-Egervary theorem.)
- Let G be a bipartite graph with bipartition (X,Y). Show that the following three conditions are equivalent.
- Session 31: None
- Session 32: Chapter 11: Exercises 6, 7
- Session 30:
- Problems Assigned in the Textbook
- Chapter 11: Exercise 30. Hint. Consider the operation ⊕ as used in the proof of Theorem 11.14 on page 260.
- Chapter 11: Exercises 23, 24
- Additional Problems
- (A17) Let G be a bipartite graph for which a maximum matching has n edges. What is the smallest possible size of a maximal matching? (You need to give an example of this size and prove that no smaller size is possible in any bipartite graph for which a maximum matching has n edges.)
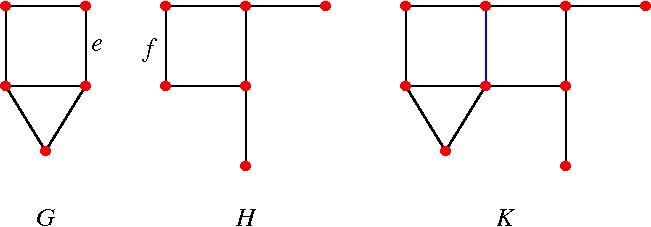
- (A18) Let G and H be finite graphs. Let K consist of the union of G and H, with an edge e of G identified with an edge f of H. (Thus if G has q edges and H has r edges, then K has q+r-1 edges.) Express the chromatic polynomial of K in terms of those of G and H. Example:
- Bonus Problems
- (B4) Let M be an n×n matrix of nonnegative integers. What is the least positive integer f(n) with the following property? If every row and column of M sums to f(n), then there exists n entries of M, no two in the same row and column, and all greater than one. For instance f(2)=3 and f(3)=5. The matrix with rows [2,1,1], [2,1,1], [0,2,2] shows that f(3)>4.
