
Session Overview
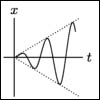 |
In this session we study the undamped harmonic oscillator forced at its natural frequency. In this case the system responds by oscillating with an amplitude that grows to infinity over time. This is what is called pure resonance. Mathematically it is the case p(a) = 0 in the Exponential Response Formula. |
Session Activities
Read the course notes:
- Pure Resonance: Introduction (PDF)
- The Exponential Response Formula: Resonant Case (PDF)
- Undamped Forced Systems (PDF)
Watch the lecture video clips:
- Resonance in the Undamped System (00:18:22)
-
Reconciling the Resonant and Non-resonant Solutions (00:16:03)
Reconciling the Resonant and Non-resonant Solutions
> Download from iTunes U (MP4 - 85MB)
> Download from Internet Archive (MP4 - 85MB)
Watch the problem solving video:
- Pure Resonance (00:11:17)
Check Yourself
Complete the problem set:
