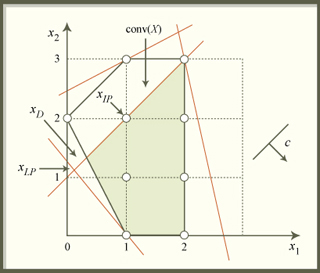
An example of Lagrangean duality, discussed in Lecture 8. (Image by Prof. Bertsimas.)
Instructor(s)
Prof. Dimitris Bertsimas
Prof. Andreas Schulz
MIT Course Number
15.083J / 6.859J
As Taught In
Fall 2009
Level
Graduate
Course Description
Course Features
Course Description
The course is a comprehensive introduction to the theory, algorithms and applications of integer optimization and is organized in four parts: formulations and relaxations, algebra and geometry of integer optimization, algorithms for integer optimization, and extensions of integer optimization.
Other Versions
Other OCW Versions
Archived versions: ![]()


