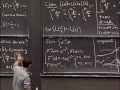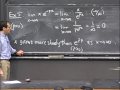Lecture 27: Trig Integrals

Related Resources

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation, or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: Well, because our subject today is trig integrals and substitutions, Professor Jerison called in his substitute teacher for today. That's me. Professor Miller. And I'm going to try to tell you about trig substitutions and trig integrals. And I'll be here tomorrow to do more of the same, as well. So, this is about trigonometry, and maybe first thing I'll do is remind you of some basic things about trigonometry.

So, if I have a circle, trigonometry is all based on the circle of radius 1 and centered at the origin. And so if this is an angle of theta, up from the x-axis, then the coordinates of this point are cosine theta and sine theta. And so that leads right away to some trig identities, which you know very well. But I'm going to put them up here because we'll use them over and over again today. Remember the convention sin^2 theta secretly means (sin theta)^2. It would be more sensible to write a parenthesis around the sine of theta and then say you square that. But everybody in the world puts the 2 up there over the sin, and so I'll do that too.

So that follows just because the circle has radius 1. But then there are some other identities too, which I think you remember. I'll write them down here. cos(2theta), there's this double angle formula that says cos(2theta) = cos^2(theta) - sin^2(theta). And there's also the double angle formula for the sin(2theta). Remember what that says? 2 sin(theta) cos(theta). I'm going to use these trig identities and I'm going to use them in a slightly different way. And so I'd like to pay a little more attention to this one and get a different way of writing this one out. So this is actually the half angle formula. And that says, I'm going to try to express the cos(theta) in terms of the cos(2theta). So if I know the cos(2theta), I want to try to express the cos theta in terms of it. Well, I'll start with a cos(2theta) and play with that.

OK. Well, we know what this is, it's cos^2(theta) - sin^2(theta). But we also know what the sin^2(theta) is in terms of the cosine. So I can eliminate the sin^2 from this picture. So this is equal to cos^2(theta) minus the quantity 1 - cos^2(theta). I put in what sin^2 is in terms of cos^2 And so that's 2 cos^2(theta) - 1. There's this cos^2, which gets a plus sign. Because of these two minus signs. And there's the one that was there before, so altogether there are two of them.

I want to isolate what cosine is. Or rather, what cos^2 is. So let's solve for that. So I'll put the 1 on the other side. And I get 1 + cos(2theta). And then, I want to divide by this 2, and so that puts a 2 in this denominator here. So some people call that the half angle formula. What it really is for us is it's a way of eliminating powers from sines and cosines. I've gotten rid of this square at the expense of putting in a 2theta here. We'll use that. And, similarly, same calculation shows that sin^2(theta) = (1 - cos(2theta)) / 2. Same cosine, in that formula also, but it has a minus sign. For the sin^2.

OK. so that's my little review of trig identities that we'll make use of as this lecture goes on. I want to talk about trig identity-- trig integrals, and you know some trig integrals, I'm sure, already. Like, well, let me write the differential form first. You know that d sin theta, or maybe I'll say d sin x, is, let's see, that's the derivative of sin x times dx, right. The derivative of sin x is cos x, dx. And so if I integrate both sides here, the integral form of this is the integral of cos x dx. Is sin x plus a constant. And in the same way, d cos x = -sin x dx. Right, the derivative of the cosine is minus sine. And when I integrate that, I find the integral of sin x dx is -cos x + c. So that's our starting point. And the game today, for the first half of the lecture, is to use that basic-- just those basic integration formulas, together with clever use of trig identities in order to compute more complicated formulas involving trig functions.

So the first thing, the first topic, is to think about integrals of the form sin^n (x) cos^n (x) dx. Where here I have in mind m and n are non-negative integers. So let's try to integrate these. I'll show you some applications of these pretty soon. Looking down the road a little bit, integrals like this show up in Fourier series and many other subjects in mathematics. It turns out they're quite important to be able to do. So that's why we're doing them now. Well, so there are two cases to think about here. When you're integrating things like this. There's the easy case, and let's do that one first. The easy case is when at least one exponent is odd. That's the easy case. So, for example, suppose that I wanted to integrate, well, let's take the case m = 1. So I'm integrating sin^n (x) cos x dx. I'm taking-- Oh, I could do that one. Let's see if that's what I want to take. Yeah. My confusion is that I meant to have this a different power. You were thinking that.

So let's do this case when m = 1. So the integral I'm trying to do is any power of the sine times the cosine. Well, here's the trick. Recognize, use this formula up at the top there to see cos x dx as something that we already have on the blackboard. So, the way to exploit that is to make a substitution. And substitution is going to be u = sin x. And here's why. Then this integral that I'm trying to do is the integral of u^n, that's already a simplification. And then there's that cos x dx. When you make a substitution, you've got to go all the way and replace everything in the expression by things involving this new variable that I've introduced. So I'd better get rid of the cos x dx and rewrite it in terms of du or in terms of u. And I can do that because du, according to that formula, is cos x dx. Let me put a box around that. That's our substitution. When you make a substitution, you also want to compute the differential of the variable that you substitute in. So the cos x dx that appears here is just, exactly, du. And I've replaced this trig integral with something that doesn't involve trig functions at all. This is a lot easier. We can just plug into what we know here. This is u^(n+1) / (n+1) plus a constant, and I've done the integral.

But I'm not quite done with the problem yet. Because to be nice to your reader and to yourself, you should go back at this point, probably, go back and get rid of this new variable that you introduced. You're the one who introduced this variable, you. Nobody except you, really, knows what it is. But the rest of the world knows what they asked for the first place that involved x. So I have to go back and get rid of this. And that's not hard to do in this case, because u = sin x. And so I make this back substitution. And that's what you get. So there's the answer.

OK, so the game was, I use this odd power of the cosine here, and I could see it appearing as the differential of the sine. So that's what made this substitution work. Let's do another example to see how that works out in a slightly different case. So here's another example. Now I do have an odd power. One of the exponents is odd, so I'm in the easy case. But it's not 1. The game now is to use this trig identity to get rid of the largest even power that you can, from this odd power here. So use sin^2 x = 1 - cos^2 x, to eliminate a lot of powers from that odd power. Watch what happens. So this is not really a substitution or anything, this is just a trig identity. This sine cubed is sine squared times the sine. And the sine squared is 1 - cos^2 x. And then I have the remaining sin x. And then I have cos^2 x dx. So let me rewrite that a little bit to see how this works out. This is the integral of cos^2 x minus, and then there's the product of these two. That's cos^4 x times sin x dx.

So now I'm really exactly in the situation that I was in over here. I've got a single power of a sine or cosine. It happens that it's a sine here. But that's not going to cause any trouble, we can go ahead and play the same game that I did there. So, so far I've just been using trig identities. But now I'll use a trig substitution. And I think I want to write these as powers of a variable. And then this is going to be the differential of that variable. So I'll take u to be cos x, and that means that du = -sin x dx. There's the substitution. So when I make that substitution, what do we get. Cosine squared becomes u^2. Cosine to the 4th becomes u^4, and sin x dx becomes not quite du, watch for the signum, watch for this minus sign here. It becomes -du. But that's OK. The minus sign comes outside. And I can integrate both of these powers, so I get -u^3 / 3. And then this 4th power gives me a 5th power, when I integrate. And don't forget the constant. Am I done? Not quite done. I have to back substitute and get rid of my choice of variable, u, and replace it with yours. Questions?

STUDENT: [INAUDIBLE]

PROFESSOR: There should indeed. I forgot this minus sign when I came down here. So these two gang up to give me a plus. Was that what the other question was about, too? Thanks. So let's back substitute. And I'm going to put that over here. And the result is, well, I just replace the u by cosine of x. So this is - -cos^3(x) / 3 plus, thank you, cos^5(x) / 5 + c. And there's the answer. By the way, you can remember one of the nice things about doing an integral is it's fairly easy to check your answer. You can always differentiate the thing you get, and see whether you get the right thing when you go back. It's not too hard to use the power rules and the differentiation rule for the cosine to get back to this if you want to check the work.

Let's do one more example, just to handle an example of this easy case, which you might have thought of at first. Suppose I just want to integrate a cube. sin^3 x. No cosine in sight. But I do have an odd power of a trig function, of a sine or cosine. So I'm in the easy case. And the procedure that I was suggesting says I want to take out the largest even power that I can, from the sin^3. So I'll take that out, that's a sin^2, and write it as 1 - cos^2. Well, now I'm very happy. Because it's just like the situation we had somewhere on the board here. It's just like the situation we had up here. I've got a power of a cosine times sin x dx.

So exactly the same substitution steps in. You get, and maybe you can see what happens without doing the work. Shall I do the work here? I make the same substitution. And so this is (1 - u (1 - u^2) times -du. Which is u - u^3 / 3. But then I want to put this minus sign in place, and so that gives me -u + u^3 / 3 plus a constant. And then I back substitute and get cos x + cos^3 x / 3. So this is the easy case. If you have some odd power to play with, then you can make use of it and it's pretty straightforward.

OK the harder case is when you don't have an odd power. So what's the program? I'm going to do the harder case, and then I'm going to show you an example of how to integrate square roots. And do an application, using these ideas from trigonometry. So I want to keep this blackboard. Maybe I'll come back and start here again. So the harder case is when they're only even exponents. I'm still trying to integrate the same form. But now all the exponents are even. So we have to do some game. And here the game is use the half angle formula. Which I just erased, very sadly, on the board here. Maybe I'll rewrite them over here so we have them on the board. I think I remember what they were.

So the game is I'm going to use that half angle formula to start getting rid of those even powers. Half angle formula written like this, exactly, talks about-- it rewrites even powers of sines and cosines. So let's see how that works out in an example. How about just the cosine squared for a start. What to do? I can't pull anything out. I could rewrite this as 1 - sin^2, but then I'd be faced with integrating the sin^2, which is exactly as hard. So instead, let's use this formula here. This is really the same as (1+cos(2theta)) / 2. And now, this is easy. It's got two parts to it. Integrating one half gives me theta over-- Oh. Miraculously, the x turned into a theta. Let's put it back as x. I get x/2 by integrating 1/2. So, notice that something non-trigonometric occurs here when I do these even integrals. x/2 appears. And then the other one, OK, so this takes a little thought. The integral of the cosine is the sine, or is it minus the sine. Negative sine. Shall we take a vote? I think it's positive. And so you get sin(2x), but is that right? Over 2. If I differentiate the sin(2x), this 2 comes out. And would give me an extra 2 here. So there's an extra 2 that I have to put in here when I integrate it. And there's the answer.

This is not a substitution. I just played with trig identities here. And then did a simple trig integral, getting your help to get the sign right. And thinking about what this 2 is going to do. It produces a 2 in the denominator. But it's not applying any complicated thing. It's just using this identity. Let's do another example that's a little bit harder.

This time, sin^2 times cos^2. Again, no odd powers. I've got to work a little bit harder. And what I'm going to do is apply those identities up there. Now, what I recommend doing in this situation is going over to the side somewhere. And do some side work. Because it's all just playing with trig functions. It's not actually doing any integrals for a while. So, I guess one way to get rid of the sin^2 and the cos^2 is to use those identities and so let's do that. So the sine is (1 - cos(2x)) / 2. And the cosine is (1 + cos(2x)) / 2. So I just substitute them in. And now I can multiply that out. And what I have is a difference times a sum. So you know a formula for that. Taking the product of these two things, well there'll be a 4 in the denominator. And then in the numerator, I get the square of this minus the square of this. (a-b)(a+b) = a^2 - b^2. = - So I get that. Well, I'm a little bit happier, because at least I don't have 4. I don't have 2 different squares. I still have a square, and want to integrate this. I'm still not in the easy case. I got myself back to an easier hard case. But we do know what to do about this. Because I just did it up there. And I could play into this formula that we got. But I think it's just as easy to continue to calculate here. Use the half angle formula again for this, and continue on your way.

So I get a 1/4 from this bit. And then minus 1/4 of cos^2(2x). And when I plug in 2x in for theta, there in the top board, I'm going to get a 4x on the right-hand side. So it comes out like that. And I guess I could simplify that a little bit more. This is a 1/4. Oh, but then there's a 2 here. It's half that. So then I can simplify a little more. It's 1/4 - 1/8, which is 1/8. And then I have 1/8 cos(4x).

OK, that's my side work. I just did some trig identities over here. And rewrote sine squared times cosine squared as something which involves just no powers of trig, just cosine by itself. And a constant. So I can take that and substitute it in here. And now the integration is pretty easy. 1/8, cos(4x) / 8, dx, which is, OK the 1/8 is going to give me x/8. The integral or cosine is plus or minus the sine. The derivative of the sine is plus the cosine. So it's going to be plus the-- Only there's a minus here. So it's going to be the sine-- minus sin(4x) / 8, but then I have an additional factor in the denominator. And what's it going to be? I have to put a 4 there. So we've done that calculation, too. So any of these-- If you keep doing this kind of process, these two kinds of procedures, you can now integrate any expression that has a power of a sine times a power of a cosine in it, by using these ideas. Now, let's see.

Oh, let me give you an alternate method for this last one here. I know what I'll do. Let me give an alternate method for doing, really doing the side work over there. I'm trying to deal with sin^2 times cos^2. Well that's the square of sin x cos x. And sin x cos x shows up right here. In another trig identity. So we can make use of that, too. That reduces the number of factors of sines and cosines by 1. So it's going in the right direction. This is equal to 1/2 sin(2x), squared. Sine times cosine is 1/2-- Say this right. It's sin(2x) / 2, and then I want to square that.

So what I get is sin^2(2x) / 4. Which is, well, I'm not too happy yet, because I still have an even power. Remember I'm trying to integrate this thing in the end, even powers are bad. I try to get rid of them. By using that formula, the half angle formula. So I can apply that to sin x here again. I get 1/4 of (1 - cos(4x)) / 2. That's what the half angle formula says for sin^2(2x). And that's exactly the same as the expression that I got up here, as well. It's the same expression that I have there. So it's the same expression as I have here. So this is just an alternate way to play this game of using the half angle formula.

OK, let's do a little application of these things and change the topic a little bit. So here's the problem. So this is an application and example of a real trig substitution. So here's the problem I want to look at. OK, so I have a circle whose radius is a. And I cut out from it a sort of tab, here. This tab here. And the height of this thing is b. So this length is a number b. And what I want to do is compute the area of that little tab. That's the problem. So there's an arc over here. And I want to find the area of this, for a and b, in terms of a and b. So the area, well, I guess one way to compute the area would be to take the integral of y dx. You've seen the idea of splitting this up into vertical strips whose height is given by a function y(x). And then you integrate that. That's an interpretation for the integral. The area is given by y dx. But that's a little bit awkward, because my formula for y is going to be a little strange. It's constant, value of b, along here, and then at this point it becomes this arc, of the circle. So working this out, I could do it but it's a little awkward because expressing y as a function of x, the top edge of this shape, it's a little awkward, and takes two different regions to express.

So, a different way to say it is to say x dy. Maybe that'll work a little bit better. Or maybe it won't, but it's worth trying. I could just as well split this region up into horizontal strips. Whose width is dy, and whose length is x. Now I'm thinking of this as a function of y. This is the graph of a function of y. And that's much better, because the function of y is, well, it's the square root of a^2 - y^2, isn't it. That's x x^2 + y^2 = a^2. So that's what x is. And that's what I'm asked to integrate, then. Square root of (a^2 - y^2), dy. And I can even put in limits of integration. Maybe I should do that, because this is supposed to be an actual number. I guess I'm integrating it from y = 0, that's here. To y = b, dy. So this is what I want to find. This is a integral formula for the area of that region.

And this is a new form. I don't think that you've thought about integrating expressions like this in this class before. So, it's a new form and I want to show you how to do it, how it's related to trigonometry. It's related to trigonometry through that exact picture that we have on the blackboard. After all, this a^2 - y^2 is the formula for this arc. And so, what I propose is that we try to exploit the connection with the circle and introduce polar coordinates. So, here if I measure this angle then there are various things you can say. Like the coordinates of this point here are a cos(theta), a-- Well, I'm sorry, it's not. That's an angle, but I want to call it theta_0. And, in general you know that the coordinates of this point are (a cos(theta), a sin(theta)). If the radius is a, then the angle here is theta. So x = a cos(theta), and y = a sin(theta), just from looking at the geometry of the circle. So let's make that substitution. y = a sin(theta). I'm using the picture to suggest that maybe making the substitution is a good thing to do. Let's follow along and see what happens.

If that's true, what we're interested in is integrating, a^2 - y^2. Which is a^2-- We're interested in integrating the square root of a^2 - y^2. Which is the square root of a^2 minus this. a^2 sin^2(theta). And, well, that's equal to a cos theta. That's just sin^2 + cos^2 = 1, all over again. It's also x. This is x. And this was x. So there are a lot of different ways to think of this. But no matter how you say it, the thing we're trying to integrate, a^2 - y^2 is, under this substitution it is a cos(theta). So I'm interested in integrating the square root of (a^2 - y^2), dy. And I'm going to make this substitution y = a sin(theta). And so under that substitution, I've decided that the square root of a^2 - y^2 is a cos(theta). That's this. What about the dy? Well, I'd better compute the dy. So dy, just differentiating this expression, is a cos(theta) d theta. So let's put that in. dy = a cos(theta) d theta. OK. Making that trig substitution, y = a sin(theta), has replaced this integral that has a square root in it. And no trig functions. With an integral that involves no square roots and only trig functions. In fact, it's not too hard to integrate this now, because of the work that we've done. The a^2 comes out. This is cos^2(theta) d theta. And maybe we've done that example already today. I think we have. Maybe we can think it through, but maybe the easiest thing is to look back at notes and see what we got before. That was the first example in the hard case that I did. And what it came out to, I used x instead of theta at the time. So this is a good step forward. I started with this integral that I really didn't know how to do by any means that we've had so far. And I've replaced it by a trig integral that we do know how to do. And now I've done that trig integral. But we're still not quite done, because of the problem of back substituting. I'd like to go back and rewrite this in terms of the original variable, y. Or, I'd like to go back and rewrite it in terms of the original limits of integration that we had in the original problem.

In doing that, it's going to be useful to rewrite this expression and get rid of the sin(2theta). After all, the original y was expressed in terms of sin(theta), not sin(2theta). So let me just do that here, and say that this, in turn, is equal to a^2 theta / 2 plus, well, sin(2theta) = 2 sin(theta) cos(theta). And so, when there's a 4 in the denominator, what I'll get is sin(theta) cos(theta) / 2. I did that because I'm getting closer to the original terms that the problem started with. Which was sin(theta).

So let me write down the integral that we have now. The square root of a^2 - y^2, dy is, so far, what we know is a^2 (theta / 2 + sin(theta) cos(theta) / 2) + c. But I want to go back and rewrite this in terms of the original value. The original variable, y. Well, what is theta in terms of y? Let's see. y in terms of theta was given like this. So what is theta in terms of y? Ah. So here the fearsome arcsine rears its head, right? Theta is the angle so that y = a sin(theta). So that means that theta is the arcsine, or sine inverse, of y/a. So that's the first thing that shows up here. arcsin(y/a), all over 2. That's this term. Theta is arcsin(y/a) / 2. What about the other side, here? Well sine and cosine, we knew what they were in terms of y and in terms of x, if you like. Maybe I'll put the a^2 inside here. That makes it a little bit nicer. Plus, and the other term is a^2 sin(theta) cos(theta). So the a sin(theta) is just y. Maybe I'll write this (a sin(theta)) (a cos(theta)) / 2 + c. And so I get the same thing. And now here a sin(theta), that's y. And what's the a cos(theta)? It's x, or, if you like, it's the square root of a^2 - y^2. And so there I've rewritten everything, back in terms of the original variable, y. And there's an answer.

So I've done this indefinite integration of a form-- of this quadratic, this square root of something which is a constant minus y^2. Whenever you see that, the thing to think of is trigonometry. That's going to play into the sin^2 + cos^2 identity. And the way to exploit it is to make the substitution y = a sin(theta). You could also make a substitution y = a cos(theta), if you wanted to. And the result would come out to exactly the same in the end.

I'm still not quite done with the original problem that I had, because the original problem asked for a definite integral. So let's just go back and finish that as well. So the area was the integral from 0 to b of this square root. So I just want to evaluate the right-hand side here. The answer that we came up with, this indefinite integral. I want to evaluate it at 0 and at b. Well, let's see. When I evaluate it at b, I get a^2 arcsin(b/a) / 2 plus y, which is b, times the square root of a^2 - b^2, putting y = b, divided by 2. So I've plugged in y = b into that formula, this is what I get. Then when I plug in y = 0, well the, sine of 0 is 0, so the arcsine of 0 is 0. So this term goes away. And when y = 0, this term is 0 also. And so I don't get any subtracted terms at all. So there's an expression for this.

Notice that this arcsin(b/a), that's exactly this angle. arcsin(b/a), it's the angle that you get when y = b. So this theta is the arcsin(b/a). Put this over here. That is theta_0. That is the angle that the corner makes. So I could rewrite this as a a^2 theta_0 / 2 plus b times the square root of a^2 - b^2, over 2. Let's just think about this for a minute. I have these two terms in the sum, is that reasonable? The first term is a^2. That's the radius squared times this angle, times 1/2. Well, I think that is exactly the area of this sector. a^2 theta / 2 is the formula for the area of the sector. And this one, this is the vertical elevation. This is the horizontal. a^2 - b^2 is this distance. Square root of a^2 - b^2. So the right-hand term is b times the square root of a^2 - b^2 divided by 2, that's the area of that triangle. So using a little bit of geometry gives you the same answer as all of this elaborate calculus. Maybe that's enough cause for celebration for us to quit for today.

Free Downloads

Free Streaming

• VideoLectures.net

Video

• iTunes U (MP4 - 103MB)
• Internet Archive (MP4 - 103MB)

Caption

• English-US (SRT)