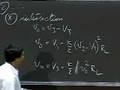Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Energy and power
Instructor: Prof. Anant Agarwal

Lecture 22: Energy and Power
Related Resources
Lecture Notes (PDF)
Demonstration: Energy and power in RC network (PDF)
Demonstration: Energy and power in CMOS (PDF)
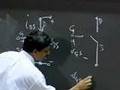
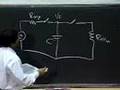
Good morning. OK. Why is it so much lower? The topic for today is Energy and Power. Most of the time this semester, up to now at least, we focused a lot on speed. We have been truly speed freaks looking at how fast can we switch the signal, what does a time domain waveform look like? We also looked at frequency responses of circuits. This week we will spend on something a little bit different, and that relates to energy and power. Energy and power is gaining a lot more importance in certainly this decade, and will do so in the future. And I am going to work out a little example towards the end of the lecture. And there you will see that if you do things naively, your handheld devices, your cell phone, laptops and so on will just up and explode. You have got to be a little bit careful in terms of how to manage energy and power. Before I get into that, I just want to wrap up with a quick review of what we covered last week. We ended last week by looking at positive feedback in analog circuits using an op amp. And, in particular, we built an oscillator. We built an oscillator that allowed us to charge a capacitor. And when the voltage across the capacitor equaled that at the minus terminal it would flip and keep doing so. And at the output you would get a waveform that looked like this. You would get a square wave output. Now, throughout the course we have talked about getting square wave inputs. And this is one example of how you can actually produce a square wave pretty much from first principles using a capacitor, resistors and an op amp. Now, I just wanted to wrap up this little item here by talking about one application of an oscillator. And this application of the oscillator really nicely closed the loop on the body of knowledge relating to digital circuits that we have covered in this course. What I want to talk about briefly is a small digital system with a sender and a receiver. And the sender is sending a signal, the receiver receives a signal, and in this course we have talked about senders sending a sequence of ones and zeros. Say, for example, the sender wants to send some sort of a signal like this. We have seen that this is quite a legitimate signal. We get some kind of oscillatory behavior because of the inductance and capacitance associated with the wire. And what you have done is that you pretty much believed me when I said that this really corresponds to a one, one, zero. The sender wants to send a one, one, zero signal to the receiver, and the receiver gets it. So this is a one, this is a one, this is a zero. But if I am a receiver, I am going to look at the square wave. There is no such thing as sending a one on a wire. You cannot send a one on a wire. You send a voltage signal or a current signal on a wire. So, the receiver receives a voltage signal. It is going to be zero for some time and then maybe 5 volts or 3 volts or whatever is your high and then zero again. How does my receiver know it's a one, one, zero? Why can't it be a one, one, one, one, zero, zero, zero? It doesn't know. How does the receiver know it's a one, one, zero sequence and not 50 ones followed by 40 zeros? It doesn't know. What we need is -- For senders to be able to communicate with receivers, we need some kind of agreed upon time when receivers sample the signal coming in and decide whether it's a one or a zero. They both have to agree on certain time bases when to look at the input. One way to deal with this is I can have a clock, a square wave signal that we call a clock in digital systems and ship it to the other side in the following manner. This clock signal can be applied to this sender and to this receiver. For more details on this, let me recommend Page 735 of the course notes that talks about a detailed example of the use of a clock in a digital system. What I can do is create a clock that looks like the square wave. The clock provides a notion of time to the circuit. And I have some kind of a clock signal generator. And I connect that to the sender and connect that to the receiver. And now both the receiver and the sender have a notion of time. And what I can do is I can tell my receiver, the sender and the receiver can have an agreement between them that says that look at the signal at your input when on the rising edge of the clock. Whenever the clock rises, when you see a rising edge look at the value in the wire and that's the value I sent. By doing so, what I can do is that the receiver can look at the signal. At this rising edge it sees a zero, this is vOH, looks up here, sees a one here, sees a one here and sees a zero. So, it correctly sampled one, one, zero at the receiving end. And the sender can send the same sequence here once we have this time base. This little brief foray circuits was simply to give you an application of a circuit that can produce a square wave. I can create a clock with a time base. Also, interestingly much more fundamental is we looked at various abstractions throughout the course. We talked about discretizing space by looking at lumped signals. What I also want to point out is that a clock can be viewed as another fundamental abstraction in the digital domain where what I am doing is discretizing time. What I am saying is that, look, in the digital domain we have already discretized value into zeros and ones, but we still had continuous time until now. And what you do in digital systems is to say that look, let's digitize everything, or rather discretize everything. And let's discretize time as well into these points that happen on the rising edge of the clock which means that the circuit has meaning, signals have meaning only when the clock is rising. That tends to discretize time which means that I really don't care what happens to signals in this time, as long as on the rising edge of the clock I get the right value. This concept is called discretizing time. And a clock lets you do that. Remember that in digital systems, which you will learn about in 004 I am really discretizing two things, discretizing values into zeros and ones, and at the same time also discretizing time into a time when I sample things and a time when I ignore values on the wires. I think you will get to clocks in 6.004 after about a month, so initially you would just be focusing on the statics of the system without worrying about any dynamic clock introduced in the circuit. OK, that's just a brief little interlude. With that let me get into today's topic of energy and power. Why is this important? The reason this is important is that what really determines the size of your handheld? You may think oh, gee, electronics in the handheld. Some of you may think, oh, the antenna in the handheld. No. What really, really determines the size and weight of your handheld devices, your PDAs, your cell phones, your laptops and so on is by and large the battery. On Page 2 I have a little cartoon that shows you that if we did not have you learn about energy and power, that's what we would all be doing in order to use cell phones. Not surprisingly the very first wireless phones ended up in automobiles because you had a big battery. And so you had these wireless phones only in cars. Because of a huge amount of research based on the knowledge, the technologies I am going to talk about in today's lecture and Thursday's lecture, you will see very simple and elegant ways of reducing the amount of battery you need to be able to get some kind of function out of analog or digital devices. I also want you to take a look at Page 2 of the handout that I have given you here, handout 63. This handout talks about the absolute latest in digital fabrication technology out there. This is not a paid commercial for IBM. IBM has a technology called CU08. It is called Blue Logic. It is called the Copper 08 Process. And in this process, if you look down on Page 1, for example, IBM claims that it can build up to 72 million gates in a single chip. With this technology they are able to build 70 to 80 million gates where a gate is, unless otherwise mentioned, pretty much defined as a two input NAND gate equivalent. So, your inverter, your NAND gate and so on count as a gate. And they can build close to 80 million of these little suckers on a single chip. Just imagine that. And the biggest chip they can build is on the order of 18 to 19 millimeters on a side, roughly two centimeters on a side. On a chip that's about one square inch. You can put down 80 million gates. What is more important for today is what is on Page 2, actually. I have circled two things on Page 2. One thing that I have circled is power supply range in the 0.7 to 1.3 volts. Notice that that voltage, the power supply voltage for these chips is significantly lower than the 5 volts that we have been normally talking about in this course. When in doubt our problems have used 5 volts. But notice that in this technology they're talking about using voltages for the power supply VS in the range of 0.7 to Well, you will find out. The second thing I've circled is something called power dissipation. And you say power dissipation is said to be 0.006 microwatts per megahertz per gate. It says power dissipation is 6 nanowatts per megahertz per gate. What that says is that each gate off your circuit will dissipate this much power at a 1 megahertz frequency. And the implication of that is that you should be able to convert that single number to the power dissipation in any chip that you might build depending on the number of gates that you have, the frequency you run the circuit at, the voltage that you use and so on and so forth. By the end of today's lecture you will be able to take this number and correlate that into the power dissipation of any chip that you might want to build with this. That just serves as the motivation that by the end of this lecture you will understand how to very quickly in five seconds or less, boom, given a chip, oh, yeah, that should consume about 30 watts of power. And what you will also do, based on some examples here, estimate the power of not the Pentium IV but a chip following the Pentium VI, let's call it the Pentium V would consume if it ran at 1 gigahertz. We will come up with some absolutely shocking numbers based on what you have learned. With that kind of motivation let me get into talking about some theory and get into the foundations of energy and power. Let's go to Page 3. To drive the theoretical discussion, I would like to focus on the energy dissipated in a MOSFET gate. And fundamentally we will talk about looking at energy and power in circuits containing switches, resistors and capacitors. The MOSFET gate is simply an illustrative example to drive the theory. But fundamentally what I am going to show you, or lead you through today, I will tell you how to compute the power and energy when you have capacitors, resistors, voltage sources and switches in your circuit. We will look at a circuit that looks like this. Your vanilla inverter circuit. My inverter. I apply some vIN signal here. It could be a square wave. It could be some sequence of ones and zeros. And this is an inverter that we all know and love. And this guy here is, stuck in a capacitor here. And this capacitor is meant to model the input gate capacitance of whatever this inverter drives plus any capacitance of the wire leading up to that gate and so on. It is just a lumped capacitor that I have stuck on there. I am interested in determining a few things. One is what we call the standby power. You will see all these terms being used in cell phones and so on. In your cell phone, your cell phone manufacturer gives you two numbers. Of course both are over exaggerations, but they give you two numbers nonetheless. One number is the number of days that the cell phone battery will last when in standby mode, right? That's exactly where standby comes from. In standby mode, how much power does your cell phone or how long will the battery last, that's the standby power. And the second thing is what we call active use power. Active use is when you are making a phone call and so on, what is the power consumed? And there again your manufacturer of your cell phone will give you a much smaller number for the active use power of your cell phone. What I am going to do is assume for discussion that the inverter is driven by a square wave signal of the following sort. This is vIN. And I am going to drive this with a signal of this sort. The period applied at the input, so I am switching the inverter on and off, on and off, on and off. And T1 seconds for the high, T2 seconds for the low. This is the inverter, this is the input signal, and we'll keep coming back to that again and again. Rather than directly taking this circuit and analyzing its power, I would like to do things in a slightly roundabout manner. What I would like to do is show you some very simple circuits and analyze their standby and active powers. And then show you that this circuit simply is a combination of some of the simple things that you have seen. Example 1. I would like to take a simple circuit that looks like this. A voltage source V applied across a resistor R, some current I. And if I apply a voltage across this resistor, that voltage would simply appear across the resistor. And the power is simply given by VI which is simply V squared divided by R. This is 6.002 101 in the very first chapter. That is the power that is dissipated by this resistor, simply V squared divided by R. That's the power dissipated by the resistor. Where does that power come from? The voltage source supplies the power. So, this guy here supplies this power and this guy here dissipates it. What is the energy that I dissipate in T time? Remember, power is the rate of energy dissipation. And so energy is simply power multiplied by time. For a circuit like this, energy dissipated in time T is simply VIT. For our gate remember we have two situations. We have VS, we have RL we have RON, vO and vIN. So, vIN is high. If vIN is high with respect to ground then RON, the switch is on, and this is the circuit that I see. In this situation the power consumed is simply V squared divided by the resistance here. It is simply VS squared divided by RL plus RON. Let me mark that with an asterisk. I will refer to this later. Similarly, when vIN is low the MOSFET is off. And the power is simply zero. I have no current flowing down and the power is zero. Absolutely basic stuff. Absolutely basic. So, the power, when I have the MOSFET on, for the kind of inverters you have seen so far, this is the power consumed by the inverter. And this asterisk here is simply to say hold that thought, we will get back to it a little later. Let me work out a second example. In this second example, I would like to consider the following circuit, a voltage source VS with a strange arrangement of switches, S1 with a resistance R1, a capacitor C in this manner, a switch S2 and a resistor R2. For now don't worry about how the circuit comes about. Just assume that I have drawn the circuit for you. And what I want to do is compute the power under certain conditions. Notice that if this is off and this is off, there is no current flowing either in this loop or this loop, and the power dissipated by the circuit is zero. But there are some arrangement of switches for which I do consume power. And so let me show you that arrangement of switches. And what I am going to do is assume that the switches open and close with the following periodic cycles. Let's assume that when this is high S1 is closed and S2 is open, and when this is low assume that S1 is open, S2 is closed. And let's assume this is T, this is T1, this is T2. That sequence should be reminiscent of this input that I am feeding to this inverter. All I am telling you here is that I am giving you the circuit. I want to compute the power consumption of the circuit. And what I am telling you is that with the frequency, with a time period of capital T, for the first T1 seconds this switch is closed and that is open. So, this circuit applies. In the second half of the clock this switch is open so this circuit applies. And what I am interested in finding out is what is the energy dissipated in each cycle of time capital T? And I also want to find out the average power. Just spend about five seconds just staring at this and kind of intuit what is going on here. I start by putting a voltage source here and I close the switch. That is open. Start by closing this, what happens? When I close the switch VS is going to charge up this capacitor. I get current flowing through my resistor, so I am going to be charging up this capacitor here. Then let's say I allow T1 to be as large as possible, and so this capacitor is going to be charged up to all of VS. After a long time this guy gets to be VS in the capacitor. And as it is charging up I have current flow through the resistor, so it is sitting there dissipating power. Notice that this sucker does not dissipate energy. It simply stores energy. So, the energy supplied by the voltage source comes in, some of it gets stored in the capacitor and some of it is being dissipated by the resistor. That gets me to the end of T1. At the end of T2 I open the switch and close this switch. When I close the switch I have some energy on the capacitor, and the voltage across the capacitor begins to drive a current through this resistor R2. And now the capacitor supplies its stored energy, and its stored energy then begins to dissipate through resistor R2. And if T2 is very long then all the charge in the capacitor drains out. And the voltage in the capacitor at the end will be zero. So, that is just sort of a high level description of what goes on. Now let's go ahead and compute from first principles the energetics of this little circuit. Let's look at the entire period capital T, and as a first step look at T1. When T1 is in place S1 is closed and S2 is open. Accordingly, the circuit that applies looks like this. I have VS, S1 is closed, so that is closed, and I have this resistance R1, I have this capacitance C, some voltage VC across the capacitor. You can go ahead and assume that VC of zero is zero. That I start off my life with no voltage across the capacitor. First of all, let me plot the waveforms and write the expressions down and then compute the energy supplied by the voltage source and then look at where the energy goes. You all know, or should know by now, if I plot VC as a function of time, remember, this is really easy to do. VC as a function of time goes like this. At time T equal to zero I am telling you that the capacitor voltage is zero. I am telling you that. So, it is at zero. And then the capacitor charges up until it reaches VS. I also know that after a long time this will be VS, after a long time that will be VS, and between those two I have a rising function that looks like this. I can similarly plot the current for you. At time T equal to zero instantaneously the capacitor looks like a short, and so the current that I start off with is going to be VS divided by R1. The voltage across the capacitor is zero. All the voltage falls across the resistor R1. So, VS divided by R1 is the initial instantaneous current. And after a long time, because VC reaches VS, the current is going to be zero. And between those two points I get an exponential decay. I could very quickly write down the expression for the current. And that is simply the initial value VS divided by R1 times the exponential decay minus T divided by the time constant for the circuit R1C. You have seen this stuff before. Here comes the part that we care about for now. Let's find out what is the total energy provided by the source. When dealing with energy computations you have to be incredibly careful of these words here, supply, provided versus dissipated. Dissipated implies that the resistor is burning energy. Provided means that the source is supplying that energy. So, energy provided by source during T1. Let's go ahead and compute that very quickly. The energy supplied by the source is simply the voltage across the source multiplied by the current being supplied by the source. This is i. Remember, by associated variables convention, if I have a voltage across some element and the current into the element is positive then that element dissipates power. If the voltage here is, say, 1 volt and it is supplying current, if the i is out in the other direction then it is supplying power. In this case, the current i is going to be on the outside, heading outside. The total energy is going to be the instantaneous power integrated over time, and that is simply VS. Remember, the instantaneous power is VS times the current i, so the instantaneous power is simply VS times i, that is the instantaneous power. To get the energy provided by source and some time, I have to integrate that instantaneous power over the period of interest T1. That gives me the energy supplied by the source during T1. And let me go ahead and substitute for i with this expression here. It is VS times i, and i is VS divided by R1 times this expression here. That gives me (VS^2/R1)e^(-t/R1C) dt. Let me carry out the integration there. I get -1/RC, so I get this outside. And I also get to write down, oops, let me do that a little bit more carefully. VS^2/R1 simply comes out and I get a -R1C in the numerator. If I differentiate it then I get R1C in the denominator. I have an integral that comes up here. And then I write down e^-t/R1C, zero and T1. So, this R1 and this R1 cancel out. And I end up getting something that looks like this. I get CVS^2. And so there is a minus sign out here, so at zero this thing goes to a one, so I get a one. And because of minus sign I get e to the -T1/R1C. All I have done here is simply go through the math to do this integration here. What I am also going to do is assume that if T1, if the time that the switch is closed is much, much bigger than the time constant of the circuit, T1 is much, much greater than R1C, if this is much, much greater than R1C then this term goes to zero. And this becomes more or less equal to CVS^2. What do we have here? What we have here is that if I let the switch stay closed for a long time and S to be open then the voltage source is going to supply some amount of energy. That energy will equal CVS^2. The voltage across the capacitor will be VS and all that energy would have been supplied by this guy. Let me pose the following conundrum here. If the voltage across the capacitor is VS, because we know the energy stored in the capacitor is half CV^2. So, the energy in the capacitor is half CVS^2. At the end of the day, since the voltage across the capacitor is VS, ΩCV@2 is the energy stored here. But we know, from this calculation, the source has supplied CVS^2. Source has supplied twice that energy. This guy has supplied twice that energy and only half of that is stored here. Who ate up the other half? The resistor, exactly. The resistor has walloped half the energy. Let me just show it to you. It dissipated ΩCVS^2. It's pretty interesting. It's a pretty simple result. If T1 is very large compared to time constant then half the energy is in the capacitor and half of it has been burned by R1. This energy has not been burned. It is simply stored. It is stored by the capacitor. And if you do simple energy conservation arithmetic here, the energy dissipated in the resistor plus that stored in the capacitor equals the energy supplied by the source. All right. Let's go to T2 now. At T2, S2 is closed and S1 is open. Let's look at the second part of the cycle when S1 is open and S2 is closed. And what is going to happen now is the left-hand part of the circuit can be ignored and I can focus on this part. So, S2 is closed. This is RC, my capacitor, this is vC. This is the circuit of interest. What is the initial condition on this? What is the value of vC initially? Start off, because remember, I allowed this capacity to charge up fully, and so initially I have VS on the capacitor. And so the energy on the capacitor initially is ΩCVS^2. That is the energy on the capacitor. This time around I won't go through an integration process like that, but you can if you like, and do it in a much similar manner to say that now let's suppose that T2 is much greater than this time constant. If T2 is much greater than R2C, this time constant. If that time is much greater than this entire, the initial voltage VS drives a current through the resistor, and after some amount of time the voltage across the capacitor goes to zero and all the energy in the capacitor gets dissipated in R. So, if T2 is much greater than R2C then energy dissipated in R2 is simply ΩCVS^2. Notice that the energy dissipated in R1, in the first half cycle is ΩCVS^2 and the second half cycle during T2, if T2 is large enough, all this energy gets dissipated in this resistor R2. And I have that expression here. So let me just say that this is E1 and let me say that this is E2. So, E1 is dissipated in the resistor and E2 is dissipated in R2 in the second half cycle. A couple of interesting things to note at this point. One is that E1 and E2 are independent of R. If the time constant is small enough compared to the time that I charge the capacitor then half the energy gets lots in the resistor, and that is simply ΩCVS^2. And if I let this discharge completely it doesn't matter what resistor I am discharging it through. That's the intuition. If I have certain energy here and I let it discharge completely it doesn't matter what this resistor is. Small or large, it doesn't matter. All this energy gets dissipated there. The rate at which the energy gets dissipated will change depending on R2. If R2 is very small then I get a burst of power initially and then a rapid decay after that, but if R2 is very large then I have a much slower release of energy. But suffice it to say that the energy dissipated, the total energy in T2 is simply ΩCVS^2. All right. Let's put T1 and T2 together and look at the total energy dissipated -- Total energy dissipated. E is simply E1 plus E2. Dissipated in each cycle. Assuming T1 and T2 are much larger than the respective time constants. And I know that this is ΩCVS^2, ΩCVS^2, so this is simply CVS^2. If I have an arrangement of switches and capacitors like that, I charge the capacitor, discharge the capacitor, charge the capacitor, discharge the capacitor. What it is saying is that in a charge/discharge cycle I am using up CVS^2 of energy. ΩCVS^2 when I charge it up and ΩCVS^2 when I discharge it. That is what I get. Let's compute the average power dissipated, P average in a cycle is simply E/T where T is the period of the square wave sequence that I have shown you out there. This is simply CVS^2 divided by T. If the period of the square wave is capital T, I can express that as a frequency. Let's say for example the period of the square wave is T, so let's say the frequency of the square wave is simply 1/T. I can also express this as C(VS^2)f. What does this say? Let me mark that as a thing to remember, the second thing to remember. One was the power that was the static power. And second is this power relating to this frequency f and the charging and discharging of the capacitor in that little circuit shown up there. So, this average power is CVS^2f. What this is saying is that if f is high, if I have high frequency of charging and discharging the capacitor then I am charging and discharging much more frequently so I am going to consume more power. Notice that at any given time there is no direct connection between the power supply and the ground. What I am doing is my capacitor is an intermediary. I am dumping some charge in the capacitor and the capacitor is dumping the charge into ground. It behaves like a switch to capacitor. And what it is doing is it is being charged and discharged at frequency f. So, it makes sense that the amount of average current that I am pumping through relates to the frequency at which I am charging and discharging the capacitor. And similarly the average power also relates to the value of the capacitor. If C is larger I dissipate more energy. And the same way with the voltage. If the voltage is higher then the power in that period, or the average power relates to CVS^2. Spend a few seconds staring at the two expressions. This power here relating to just this connection between the power supply and ground and that power out there relating to charging and discharging capacitors. Let's get back to our inverter right now. This is our inverter circuit. Let us say that I drive the input with the waveform shown here. Well, I go back to the same situation as here. I drive the input with a square wave, with T1 and T2 as the high time and the low time. The equivalent circuit for this is not exactly what we saw there. The equivalent circuit for this would look like this. I have a VS. And the VS supply is connected through RL, VS connected through RL to a capacitor C. This is my voltage vO. So, VS is always connected to ground through this resistor and capacitor in this manner. And then I have a resistor here RON corresponding to that MOSFET. And there I am switching it on and off in a way that it is on during T1 and off during T2. So, the situation here is a bit different from that simple situation I computed there. Much like I computed the power dissipation in that circuit, I can go ahead and compute the total power dissipated in this circuit. I won't do it here. The algebra tends to be a big more grubbier than what I have been through. And suffice it to say that you can show that the average power is given by (VS^2)/(2(RL+RON))+(CVS^2)f (RL^2)/(RL+RON)^2. OK? And for details I suggest that you look at section 12.3 of the course notes. Section 12.3 goes through the algebra to compute the total power dissipated by this specific circuit, and here is the expression we get. And let's take the specific situation where RL is much greater than RON. If RL is much greater than RON then I can ignore this RON here. And I get this. And out here, if I ignore RON, then RL and RL will cancel out and I get CVS^2f. If I ignore RON compared to RL this is the expression I get. Now you can see why I went through those two examples. This is exactly the power consumed by the connection between power supply and ground. And this CVS^2f is the power consumed in charging and discharging the capacitor. If you look at the circuit here it is consuming two kinds of power. One kind of power is due to the current flowing directly from VS through RL and RON to ground. Oh, this also assumes, by the way, that T1 is equal to T2. So, in this circuit there are two kinds of power. One is the power when the switch is on and I have a current flowing from VS to RL to ground. Notice I get an extra factor of two in the denominator here. And that two comes about because the connection to ground only happens half the time. It's half that power out there because I am connected to ground only when the switch is on. And that happens only half the time, and so therefore I get the VS^2/2RL. And then CVS^2f is simply the power that I consumed because I am charging and discharging the capacitor C. Notice that in this inverter circuit there are two kinds of power. One is called the standby power which is static power being consumed by the circuit, and the second power is the dynamic power because the circuit is switching up and down. This relates to star and this relates to the double star. And to demonstrate that, I have a little demonstration here that has an inverter. And I am going to up the frequency of the square way of driving the inverter. I am going to show you a few numbers so hang on for two minutes after this demo. I will give you some numbers, but I want you to go ahead and compute the numbers based on what we have seen here. And you will get suitably impressed, I promise you. This is the input fed to the inverter. This is the output of the inverter. Notice that the output of the inverter reflects some sort of an RC time constant because of the output driving the capacitor, and the same way here. I start off by showing you that on the left-hand side I am simply measuring the power being consumed by the circuit. Notice that the power being consumed is expressed by the needle being at this point here. This is a very low frequency so this is almost all standby power consumed by the inverter. The inverter is on half the time, and when it is on it is consuming power. What I am going to now is increase the frequency. As I increase the frequency driving the inverter what should happen to this needle? As I increase the frequency there that waveform should become closer and closer together. And what should happen to the needle? That should begin to go up. If I increase the frequency it should consume more and more power and the needle should start going up. So, let me do that for you. In terms of numbers there it is on top of the four on the scale in the middle. I am going to increase the frequency very slowly. Unfortunately, the sampling scope messes up the waveform. Ignore the waveform for now. Just look at the meter as I increase the frequency. Notice that I have increased the frequency by about a factor of 2 or 3. And notice here that this meter has moved. The needle has moved to the right. And I can keep doing that and the needle keeps moving to the right as I am consuming more and more power because I'm driving the inverter faster and faster and faster. That should convince you that there is a standby power and there is some power component related to frequency. This relates to your standby power in your cell phone. This relates to active use. Let me show you some numbers, and you can plug those numbers in yourself and see how much power this converter is going to consume and see if it makes sense. Assume that I have a chip with 10^8 gates. F is 1 gigahertz. That is 10^9. Assume C is 0.1 femtofarads which is 10^-16 farads. Assume VS is 5 volts. Assume RL is 10 kilo ohms. Use these numbers. Plug these numbers in here and get a sense if our modern-day circuitry used that inverter, what would be the power consumed by a chip that contains 10^8 of these gates? You will find out that you may have to use a nuclear power reactor to actually drive that chip, but go check it out for yourselves. In the next lecture we will see then how do our cell phones work, how does life go on despite this horrendous calculation here.